Does deep learning always have to reinvent the wheel?
Written by Andreas Maier.
Machine learning and in particular deep learning revolutionize the world as we know it today. We have seen tremendous advances in speech and image recognition, followed by the application of deep learning to many other domains. In many of those domains, deep learning is now the state of the art or is even going beyond it. A clear trend is that networks are growing more and more complex and more and more computationally demanding.
Today, we are building ever-increasing networks that are built on top of previous generations of network topologies. As neural networks are inherently compatible with other neural networks, we are able to combine and adapt them to new purposes. If you aim to tackle a new problem there are no clear guidelines that define an appropriate network topology. The most common approaches are to have a look at the work of others that attempted to solve similar problems or to design an entirely new topology on your own. This new design is often inspired by classical methods, but it is up to the network and the training data to learn the correct weights such that they converge to a plausible solution. As such they are even networks that learn well-known functions such as the Fourier transform from scratch. With the discrete Fourier transform being a matrix multiplication, it is often modeled as a fully connected layer. With this approach it is immediately clear that two disadvantages cannot be avoided: First, the fully connected layer introduces a lot of free parameters that may model entirely different functions. Second, the computational efficiency of a fast Fourier transform can never be reached with this approach.

If we already know that a specific function is required to solve a particular problem, it comes to our mind to ask the question of whether it would not be of advantage to include it into the structure of our network as a kind of prior knowledge. The method of Known Operator Learning investigates exactly this procedure in a new theoretical framework. While this idea seems simple and intuitive, the theoretical analysis identifies also clear advantages: First, the introduction of a known operation into a neural network always results in a lower or equal maximal training error bound. Second, the number of free parameters in the model is reduced and therewith also the size of the required training data is reduced. Another interesting observation is that any operation that allows the computation of a gradient with respect to the inputs may be embedded into a neural network. In fact, even a sub-gradient is already sufficient as we know from, e.g., max-pooling operations.
Interestingly, this piece of theory was only published in 2019. It was developed for the theoretical analysis of embedding of physical prior knowledge into neural networks. Yet, the observations also very nicely explain why we see the tremendous success of convolutional neural networks and pooling layers. In analogy to biology, we could argue that convolution and pooling operations are prior knowledge on perception. Recent work goes even further: there exist approaches that even include complicated filter functions such as Vesselness Filter or the Guided Filter into a neural network.
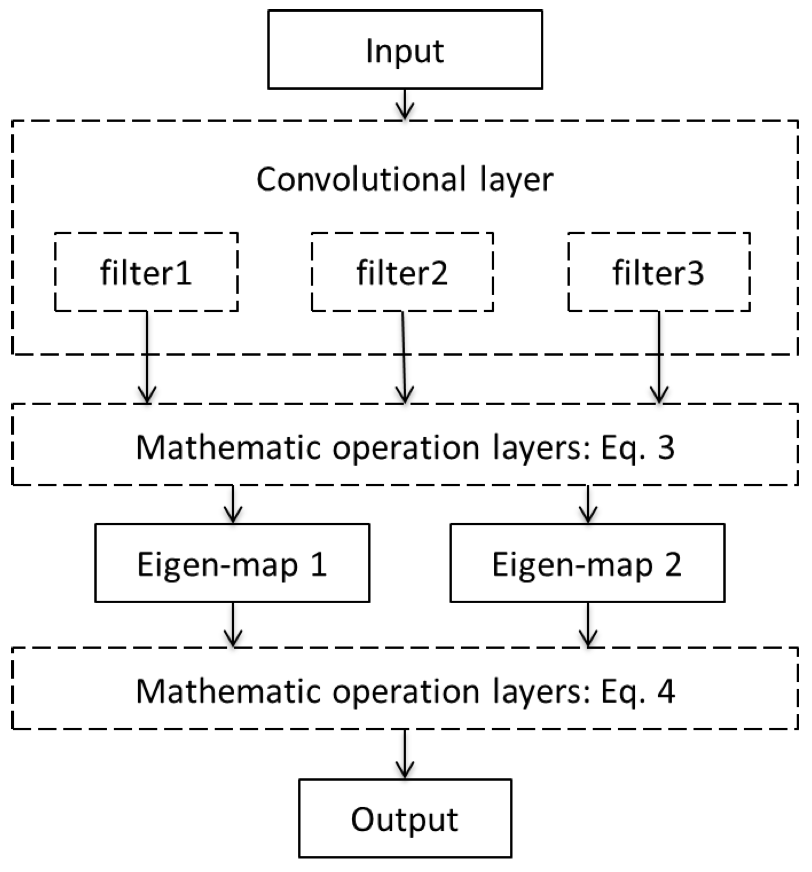
The theoretical analysis also shows that modeling errors in earlier layers are amplified by subsequent layers. This observation is also in line with the importance of feature extraction in classical machine learning and pattern analysis. A combination of feature extraction and classification as it is done in deep learning, allows us to synchronize both processes and therewith reduces the expected error after training.
As precision learning allows the combination of classical theoretical approaches and deep learning, we are now able to drive these ideas even one step further: A recent publication proposes to derive an entire neural network topography for a specific problem from the underlying physical equations. The beauty of this approach is that many of the operators and building blocks of the topology are well-known and can be implemented efficiently. Yet, they were still operations that are computationally very inefficient. However, we know from other solutions to similar problems that particular matrix inverses or other less tractable operations can be represented by other functions. In this example, an expensive matrix inverse is replaced with a circulant matrix, i.e., a convolutional layer which is the only learnable part of the proposed network. In their experiments, they demonstrate that the proposed architecture indeed tackles the problem that could previously only be approximately solved. Although they only trained on simulated data, the application on real data is also successful. Hence, the inclusion of prior knowledge also supports building network architectures that generalize well towards specific problems.
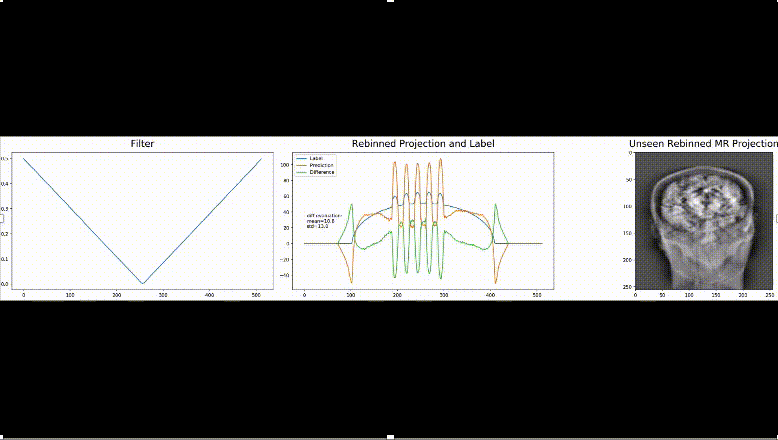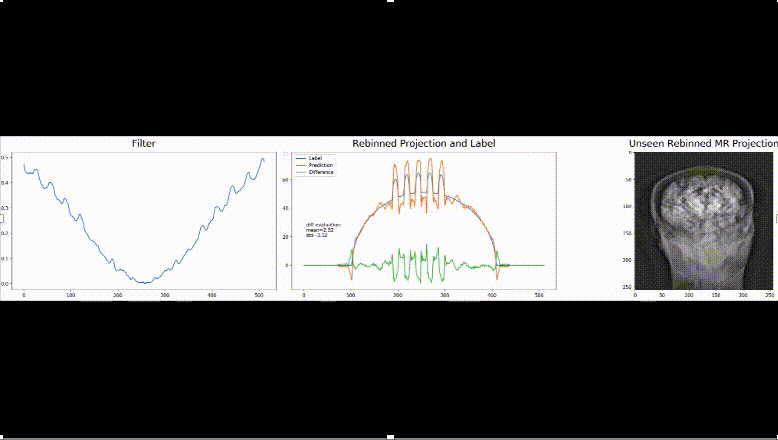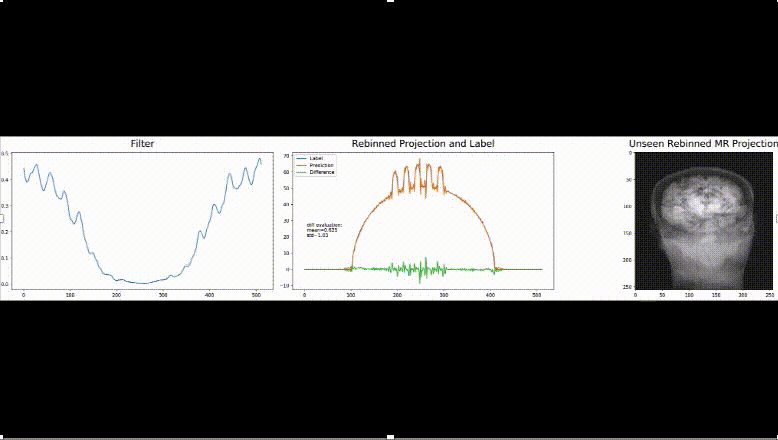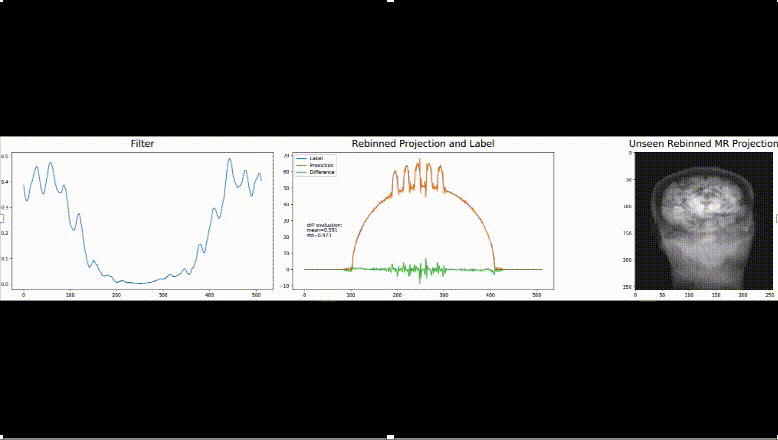
We think that these new approaches are interesting towards the community of deep learning that is going well beyond only modeling perceptual tasks today. To us, it is exciting to see that traditional approaches are inherently compatible with everything that is done today in deep learning. Hence, we believe that there are many more new developments to come in the field of machine and deep learning in the near future and it will be exciting to follow up on them.
If you think that these observations are interesting and exciting, we recommend reading our gentle introduction into deep learning as a follow up on this article (link ) or our free Deep Learning resources.
Text and images of this article are licensed under Creative Commons License 4.0 Attribution. So feel free to reuse and share any part of this work.
