You want to Learn Deep, but You don’t have Data?
Give Known Operators a try!
Written by Andreas Maier.
I am sure that all of you love Deep Learning. A major issue is though that most cool Deep Learning solutions require vast amounts of data. It easily goes into millions of training examples. I particular, if you work in medical image processing, you won’t have access to such large data sets and even if you do, good annotations may be a problem.
For these reasons, we and of course many others started looking into approaches that are not as data-hungry. In particular, I want to show you a new idea today that we coined “Known Operator Learning“. The idea has been around for quite some time but has been frowned upon by many researchers in the Machine Learning community. Let’s look at the idea first, then look at some critique, and lastly at some theoretical and experimental results which I hope you will find convincing.
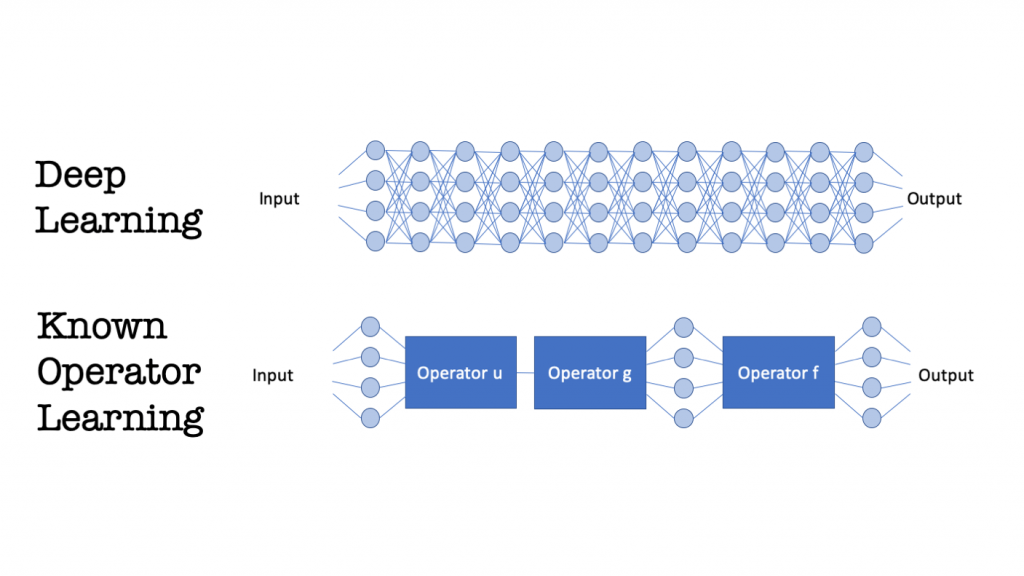
The main idea of Known Operator Learning is that we do not want to learn things that we already know. This may seem intuitive but typically triggers machine learning experts. Today’s paradigm is “the knowledge is in the data”. If you incorporate prior knowledge then you are essentially going back to the Stone Age.
What we observe in Deep Learning is quite the contrary. We see that many different architectures are being explored and the ones that show the most success are the ones that are either inspired by traditional techniques or other approaches that somehow encode knowledge about the problem into the architecture. There are also very deep approaches, but those are also related to known solutions. And all of them come with the major drawback that they require literally millions of annotated training samples.

A recent paper in Nature Machine Intelligence confirmed the intuition that prior knowledge helps in a maximal error analysis of deep networks. The authors could demonstrate that the maximal error bound is reduced with every new known operation. In the limit that all operations are known, the error is reduced to 0. Another side-effect of the inclusion of the known operations is that you reduce the number of parameters of your network which is very beneficial for the number of required training samples. While these theoretical observations are interesting, we still need some practical examples in which we can put this result to the test.

As a first example, I want to highlight Computed Tomography (CT). In CT, we typically design the scanner and its geometry is well known. The CT problem itself is rather simple because it can be expressed as a set of linear equations and solving the tomography problem is essentially connected to inverting a matrix. One problem though is that the matrix under consideration is quite big. For a common 3-D problem size with 512^3 voxels and 512 projections with 512^2 pixels each, the matrix to be inverted will require 65.000 TB of storage in floating-point precision. Therefore, simply learning the inverse matrix from scratch is not a feasible solution even in the times of deep learning.
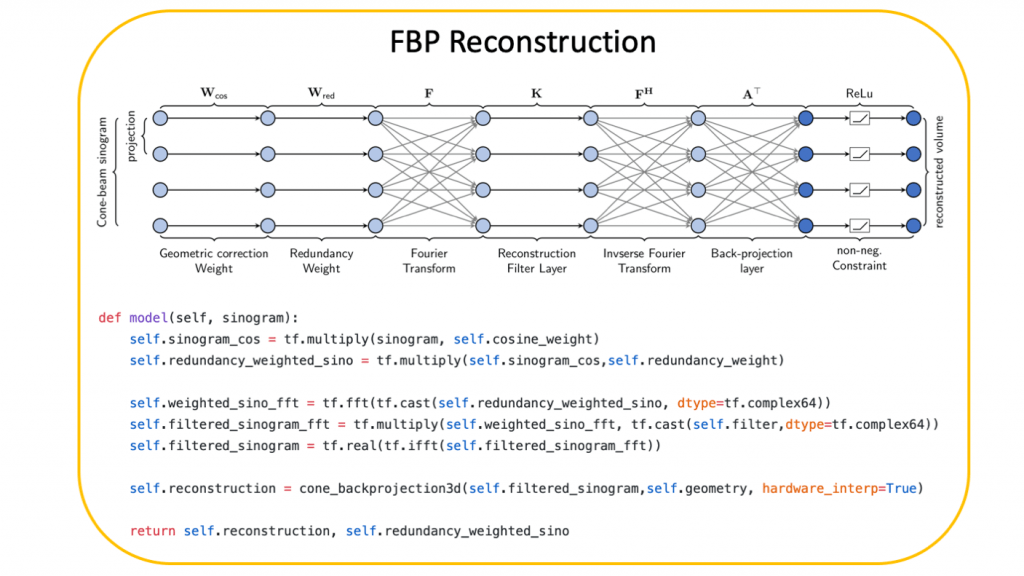
Using known operators, we can address the problem efficiently. The above example shows that the matrix inverse can be decomposed into several steps. All of the steps above have analytical solutions. However, the solutions only apply to cases in which all the required data was measured. With a combination of deep learning and our knowledge of the problem, we can now determine that the weighting matrices in the first layers are likely to be inappropriate for incomplete scans. Thus, we can arrange the known and unknown operations as layers and even use the solution to the classical problem as initialization or pre-training.
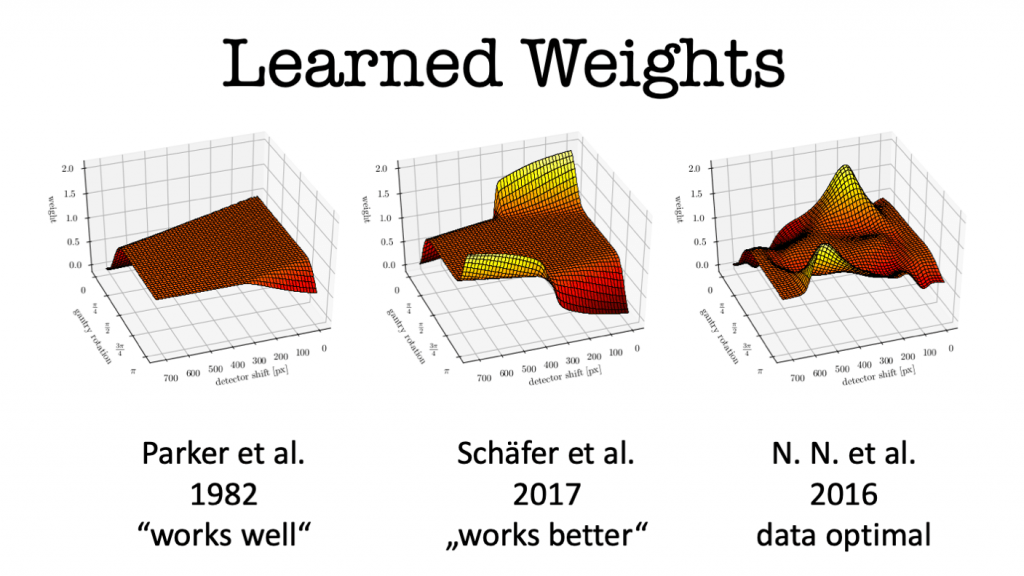
Interestingly, we can not only solve the problem this way, but we can also map the trained weights back into their original interpretation. If we do so, we can see that the initialization after Parker et al. re-trained to form the weights on the right-hand side. The neural network solution shows a striking similarity to a heuristic that was later proposed by Schäfer and colleagues. We learn from the configuration of the weights, that the rays that run through areas of insufficient measurements are amplified in order to compensate for the deterministic mass loss. Obviously, this approach can also be extended to iterative techniques as Hammernik et al. demonstrated.
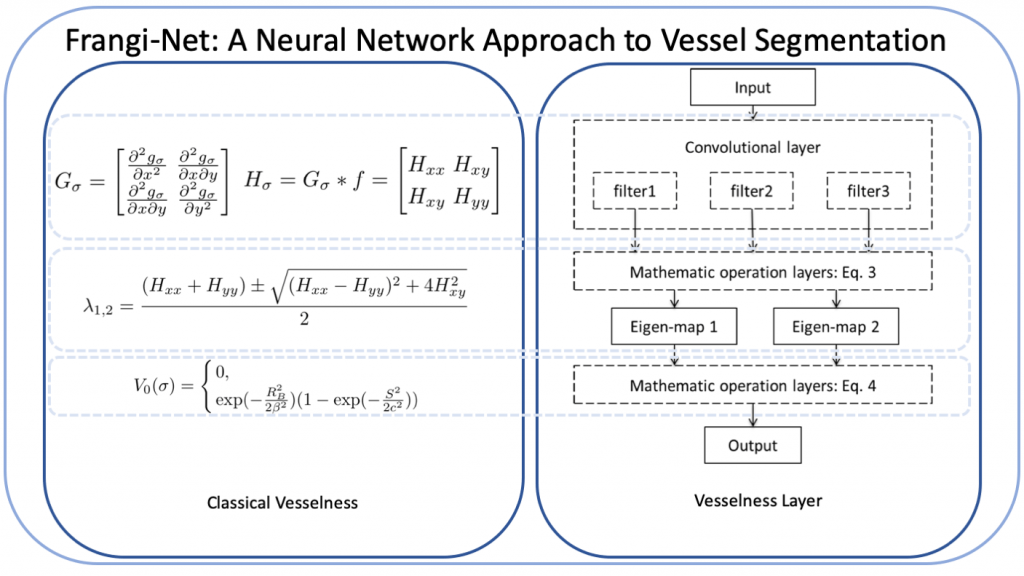
However, not all applications will allow access to such extensive prior knowledge as for the case of CT. Therefore, it is interesting to explore whether we can also re-use classical methods. Fu et al. did so in their Frangi-Net approach. This network is inspired by Frangi’s Vesselness Filter. They even demonstrated that operations such as eigenvalue computations can be expressed as layers. As such, most of the structure of the Frangi Filter can be re-used. In particular, the convolutional layers are suited for training towards a specific application. In their results, they can show that the training on a few samples indeed improves the method and allows better vessel segmentation close to the performance of U-net.

So far, we have seen that Known Operators help to make interpretable results and allow us to make classical approaches trainable with few examples. Another big problem that we typically face in Deep Learning is that results do not generalize well. We will look into this issue in one final example.
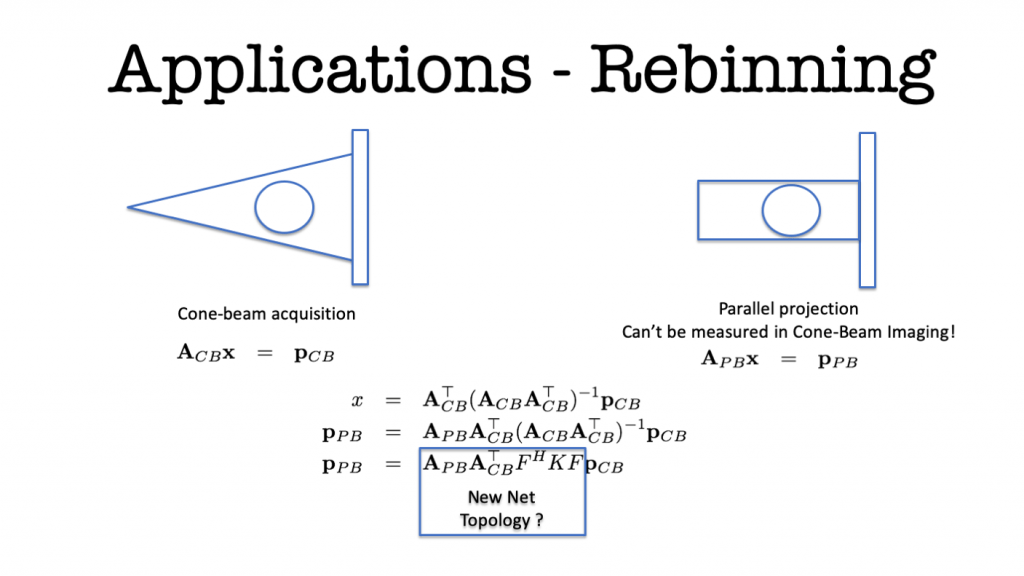
Again, we have a look at medical imaging and in particular, X-ray image formation. A typical problem is that X-ray projections can only be acquired in a projective imaging geometry that suffers from perspective distortion. In particular, in orthopedics, such location-dependent magnification is not desirable as shown on the left-hand side of the above figure. The right-hand side shows the desirable case of parallel imaging which does not suffer from magnification. Resulting images show everything as orthographic projection in which metric information is preserved and bone and crack sizes can be immediately measured without additional depth-calibration.
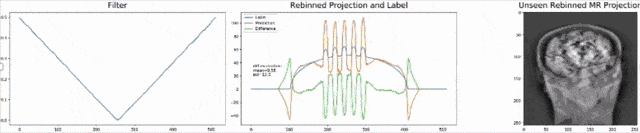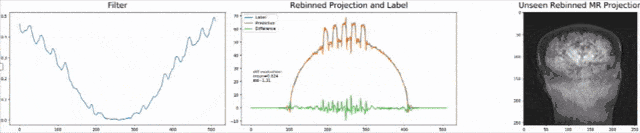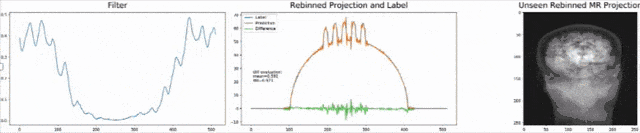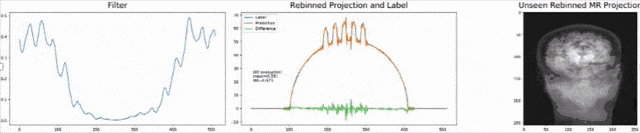
Existing approaches to solving the problem require a ray-by-ray interpolation of several projections. Doing so inherently reduces the spatial resolution of the images and therewith their diagnostic value. As both geometries can be expressed as matrix multiplications, we can solve the cone-beam projections for x and plug this into the equation for the parallel-beam projection. Unfortunately, the solution now has a large matrix inverse which is expensive to calibrate and compute in the forward pass. As we already observed in the CT solution, this step can often be expressed as convolution or point-wise multiplication in the Fourier domain. Hence, we postulate that the desired solution takes this form and go ahead and define the topology for a new network that solves the problem. Results are impressive, the filter can be trained using only synthetic examples using noise and ellipses and directly applied to new data such as the anthropomorphic phantom as shown above.

In summary, I believe that Known Operator Learning is an interesting technique for all applications in which little training data is present and well-known theory is available. For the integration into a deep network, any operation is suitable that allows the computation of a sub-gradient. As such even highly non-linear operations can be used such as the median filter. In fact, known operator learning is already on the rise for a long time, e.g. in computer vision where entire ray-tracers are introduced into deep networks. I personally hope that the known operator approach will also help to provide a better understanding of deep networks and enables their re-use without the need for transfer learning approaches. Some first results by Fu et al. indicate that this might be possible. Hence, I believe this approach is interesting and might be a good fit for problems that you want to tackle in your own work. Now go coding in our online experimentation environments and give Known Operators a try!
If you liked this essay, you can find more educational material on Deep Learning here or have a look at my YouTube Channel. This article is released under the Creative Commons 4.0 Attribution License.
