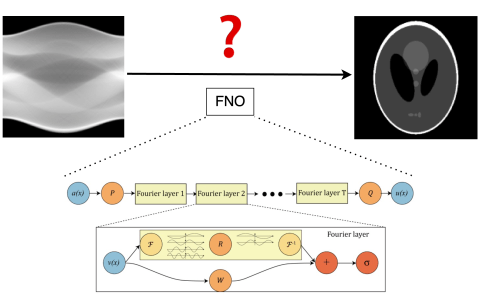
Introduction:
The aim of this project is to explore the potential of using Fourier Neural Operators (FNO) for Computed Tomography(CT) reconstruction tasks. FNO is a novel deep learning framework designed to approximate the solution of Partial Differential Equations (PDEs) by learning continuous operators using a Fourier basis. On the other hand, CT reconstruction is an important process where cross-sectional images of the objects are generated from projections obtained from X-ray scans.
CT reconstruction fundamentally represents an inverse problem, with the objective of recovering the original image from the projection data. This process can be mathematically construed through the lens of a PDE, wherein the Radon transform and its inversion emerge as central figures. By conceptualizing CT reconstruction as a PDE-solving endeavor, we aim to harness the potential of FNO to devise efficient and accurate reconstruction algorithms.
Requirements:
- Completion of at least one course on Deep Learning is mandatory.
- Proficiency in PyTorch is essential.
- Strong analytical and problem-solving skills.
Prospective candidates are warmly invited to send their CV and transcript to yipeng.sun@fau.de.
References:
- Li, Zongyi, et al. “Fourier neural operator for parametric partial differential equations.” arXiv preprint arXiv:2010.08895 (2020).
- Ongie, Gregory, et al. “Deep learning techniques for inverse problems in imaging.” IEEE Journal on Selected Areas in Information Theory 1.1 (2020): 39-56.